7 класс
Examples of my work
Кейс 1.
Как нарисовать клубнику в программе Inkscape
Как нарисовать клубнику
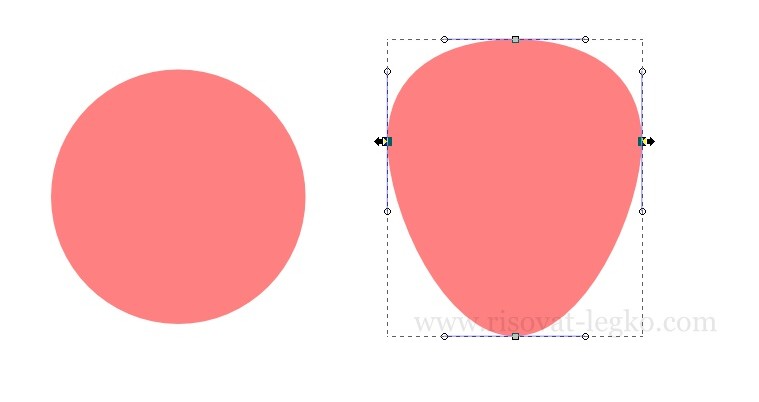
Штамповка придет нам на помощь чуть позже, а пока давайте посмотрим, как нарисовать клубнику. Для начала выведем ее форму. Рисуем круг, а затем оконтуриваем его (меню Контур — Оконтурить объект, (Ctrl+Shift+C)). Узлами выводим форму клубники.
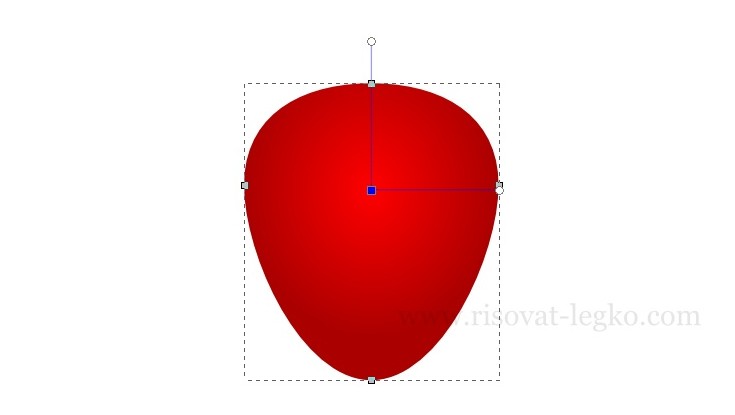
 Заливаем фигуру радиальным градиентом от светлого красного цвета, к более темному цвету. Центральная точка градиента цвет — ff0000ff, боковые точки цвет — aa0000ff.
Заливаем фигуру радиальным градиентом от светлого красного цвета, к более темному цвету. Центральная точка градиента цвет — ff0000ff, боковые точки цвет — aa0000ff.
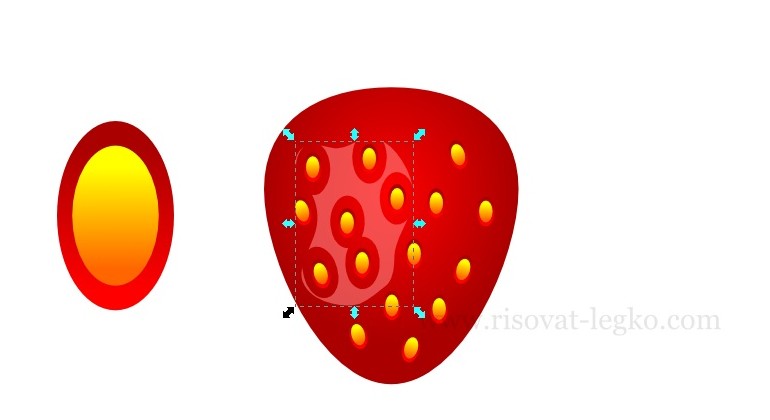
Далее в уроке как нарисовать клубнику рисуем зернышки. Создаем овал и заливаем его линейным градиентом. Цвета такие же, как и на клубнике — от темного к светлому красному цвету.
Дублируем овал (Ctrl+D), уменьшаем (<) и тоже заливаем линейным градиентом. Цвета: желтый — ffff00ff и оранжевый — ff6600ff.
Сгруппируйте оба овала в один объект (выделить оба и нажать Ctrl+G) и уменьшите его.

Когда зернышко готово, можно начать штамповку. Просто перемещайте зернышко по клубнике, не отпуская клавишу мыши, и нажимайте Пробел. На рисунке ниже вы можете видеть, сколько я наштамповал.

Следующим этапом будет рисование блика. «Кривыми Безье» и при помощи узлом создаем фигуру как на рисунке ниже.

На месте зерен рисуем овалы и располагаем как на рисунке.

Между бликом и каждым овалом проводим логическую операцию «Разность» (меню Контур – Разность (Ctrl+ -)). После этого нужно втянуть блик — меню Контур – Втянуть или Ctrl+(. Нажать два раза.
Ну и осталось в этом уроке как нарисовать клубнику нарисовать хвостик. Его мы сделаем из нескольких частей, а потом объединим в одну фигуру. На рисунке ниже вы можете видеть, какие именно фигуры я нарисовал. Для отличия придал им разные цвета.

Далее я просто все их выделяю и нажимаю (Ctrl++) или операция «Сумма» (меню Контур – Сумма). Получился симпатичный хвостик, цвет которого зеленый — 71c837ff.
Как вы видите на рисунке, я нарисовал и внутреннюю часть, цвет которой темнее — 5aa02cff. С этой задачей я предлагаю вам справиться самостоятельно.
Можно еще добавить обводку хвостику, и залить линейным градиентом. Верхняя точка градиента будет зеленого цвета — 5aa02cff, а нижняя точка прозрачная на 100%. Толщина обводки – 5.

Кейс 2.
Как нарисовать гриб поэтапно в программе Inkscape

Для начала, в уроке как нарисовать гриб, рисуем ножку и шляпку. Создаем и оконтуриваем прямоугольник (меню Контур — Оконтурить объект, (Ctrl+Shift+C)). При помощи узлов выводим форму ножки.
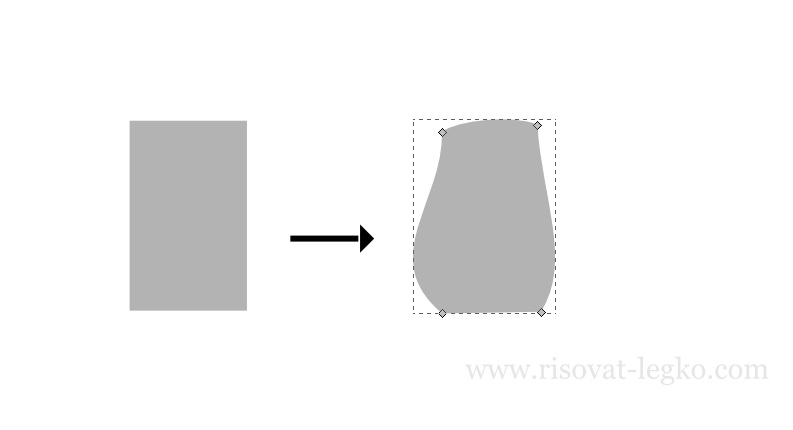
Точно таким же образом рисуем шляпку. Создаем круг, оконтуриваем и узлами выводим форму шляпки.
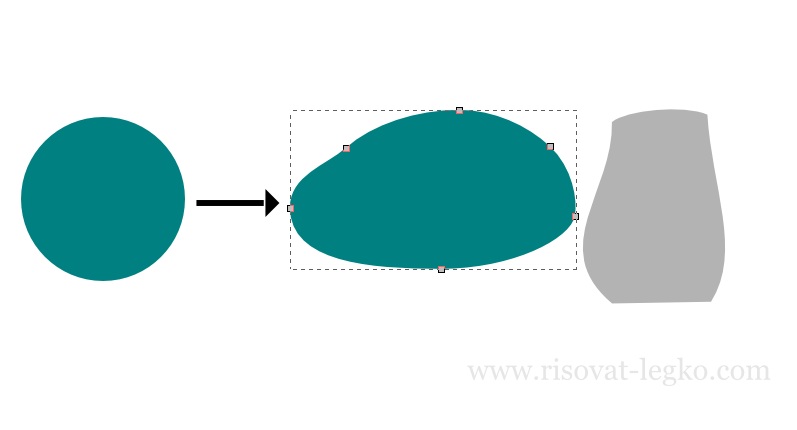
Создаем овал и располагаем его внизу шляпки.
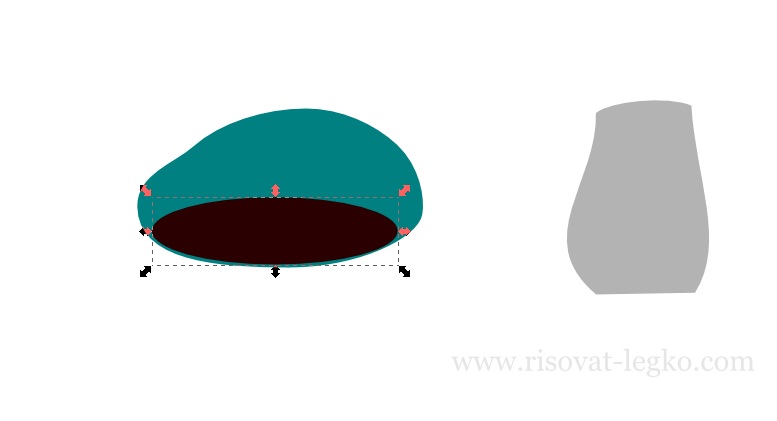
Когда все компоненты готовы, соединяем их и начинаем раскрашивать гриб. Ножка – цвет eee8e0ff.
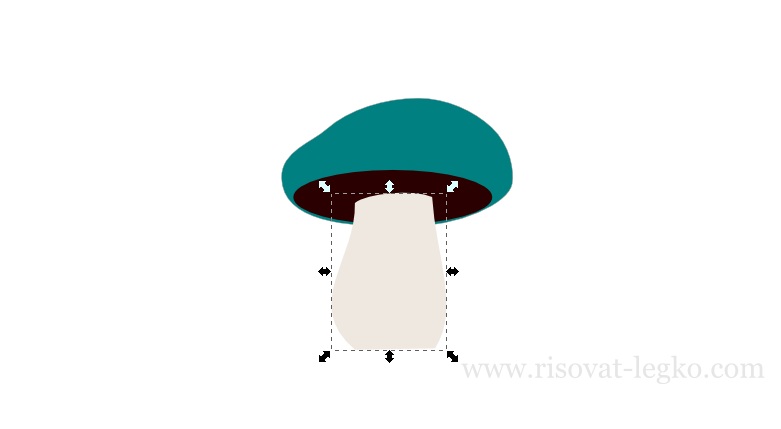
Однотонный цвет ножки гриба смотрится не очень хорошо поэтому, добавим справа еще один кусочек.
Дублируем ножку (Ctrl+D), а затем создаем фигуру, которую вы видите на рисунке ниже – она красного цвета.
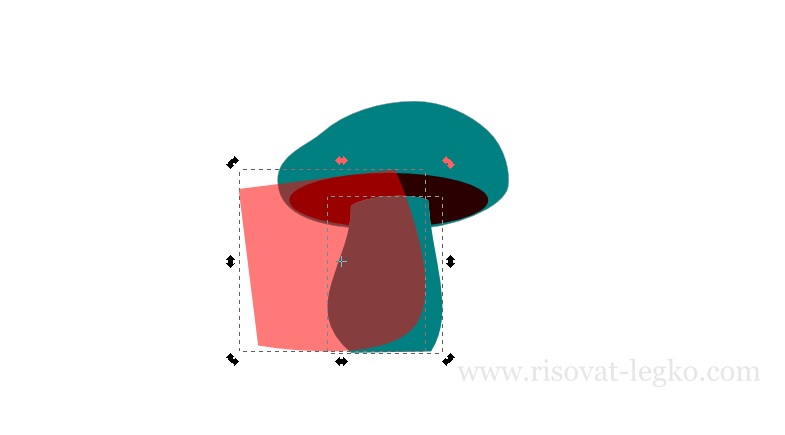
Выполняем операцию «Разность» (Ctrl+ — ). Цвет кусочка который получился — cbb9a3ff и прозрачность — 50%.

Чтобы завершить создание ножки в уроке как нарисовать гриб, нужно нарисовать тень от шляпки.
Опять же дублируем ножку (Ctrl+D), создаем фигуру нужной формы и …
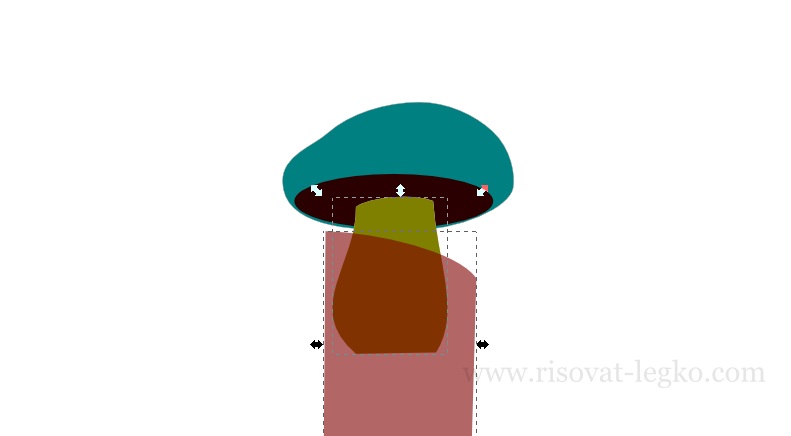
выполняем операцию «Разность» (Ctrl+ — ). Кусочек который получился заливаем линейным градиентом – верхняя точка цвет — bea78cff (непрозрачность 100%), нижняя точка цвет — e0d5c8ff (непрозрачность 0%).
Не забудьте добавить обводку ножке – толщина 1, цвет 80% grey (333333ff). При добавлении или изменении цвета обводки всегда удерживайте клавишу Shift! Если этого не делать, будет меняться цвет всей фигуры.

Переходим на шляпку и придаем ей цвет — 483e37ff. Овал внизу шляпки заливаем радиальным градиентом – центральная точка цвет — 715b30ff, боковые точки цвет — e7ca92ff.
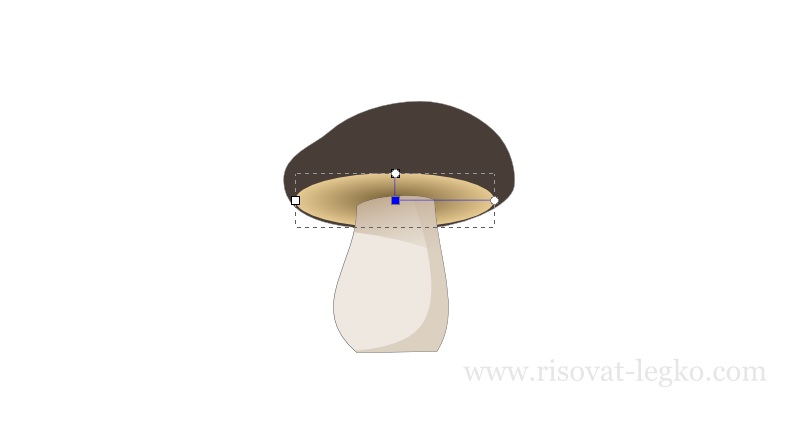
Нам осталось только добавить шляпке гриба блик. Создаем меленький овал, цвет которого — 6c5d53ff, и размещаем на шляпке.

Вместо сплошного цвета заливаем радиальным градиентом – все, гриб готов!

Теперь вы знаете, как нарисовать гриб в Inkscape. Можно еще добавить траву, которую я рисовал по такому же принципу, как и хвостик у клубники
Обобщающее повторение по теме "Работа с векторной графикой". Выполнение практических заданий на заданную тему
Рисуем поэтапно: веселая звездочка в Inkscape

Сегодня мы рисуем пошагово веселую звездочку в Inkscape. Урок совершенно не сложный и основной фигурой в нем, как вы уже догадались, будет звезда. Найти ее можно на панели инструментов слева «Рисовать звезды и многоугольники». Иконка настолько понятная, что вы без труда ее найдете. Ну что ж, нажимаем на иконку — рисовать звезды, и начинаем!
Рисуем пошагово
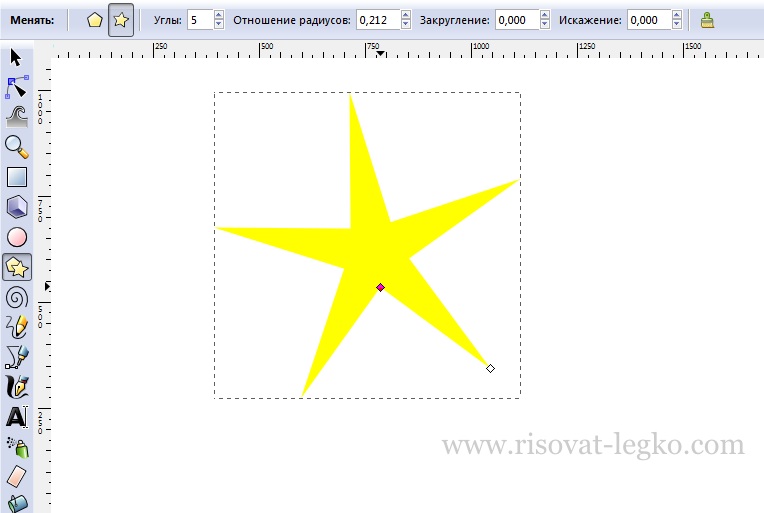
Сначала рисуем обычную пятиугольную звезду, как видите у нее острые края и наша задача закруглить углы. Это можно сделать при помощи закругления, придав значение 0,200, как на рисунке ниже. Попробуйте придать большее или меньшее значение и посмотрите что получится.
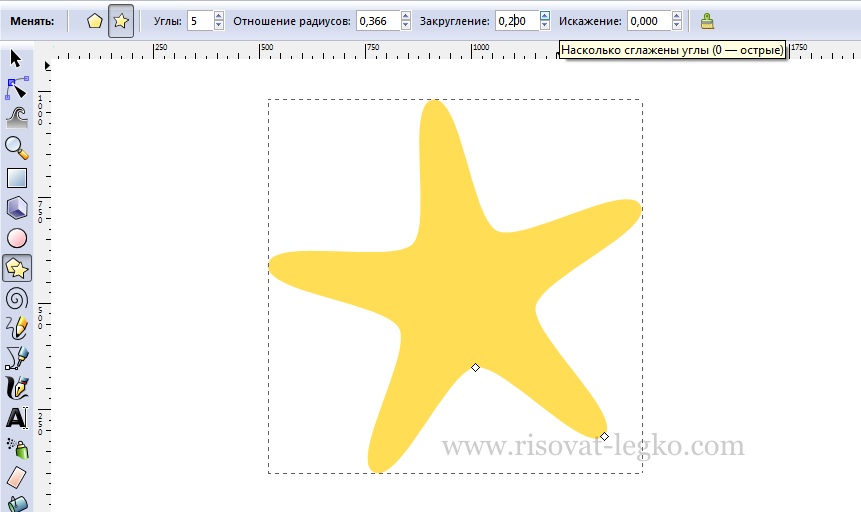
Далее нужно немного потянуть за внутренний узел, чтобы наша звездочка не была «худой». Можете придать звездочке толщину на свое усмотрение.
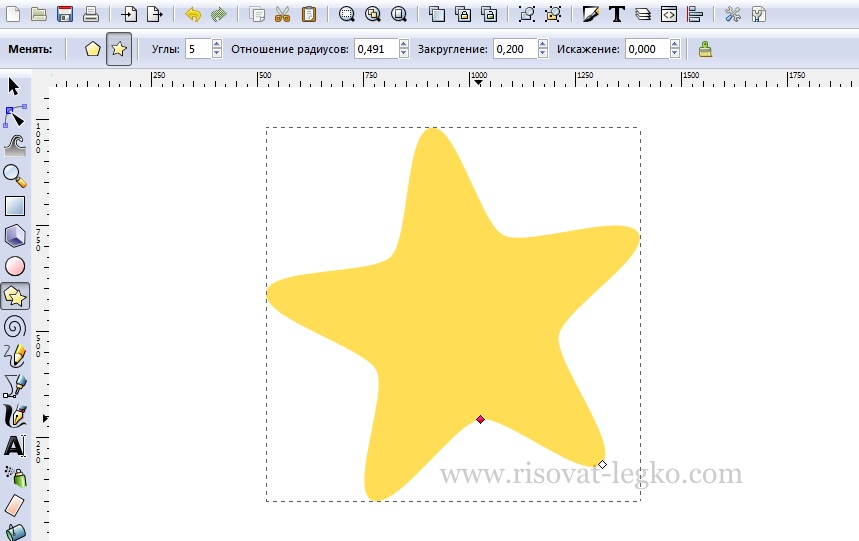
Добавляем обводку и придаем толщину в меню «Заливка и обводка – Стиль обводки» 25,000 рх. Или толщину обводки на ваше усмотрение, как вам больше нравится. Придаем обводке цвет немного темнее звездочки.
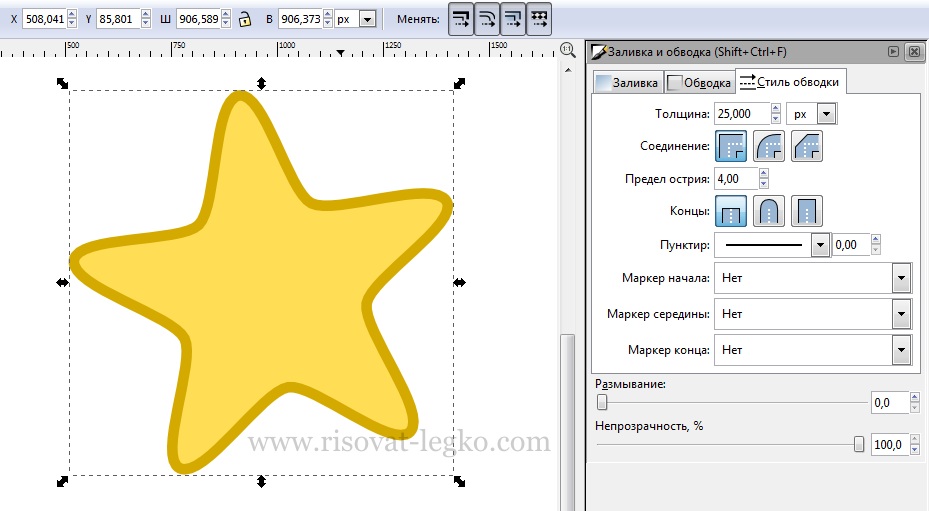
Наша звездочка готова и далее рисуем пошагово глаза. Создаем овал инструментом «Рисовать круги, эллипсы и дуги» (F5) с обводкой черного цвет и заливкой фигуры белого цвета.
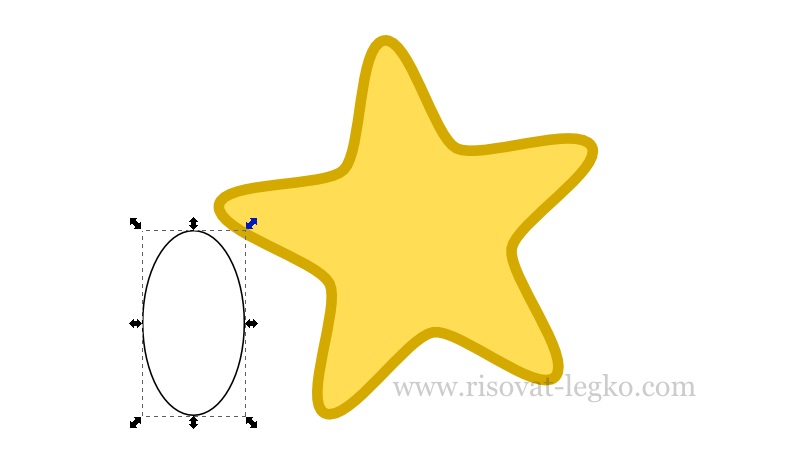
Заливаем линейным градиентом – верхняя точка белый цвет, нижняя точка серый цвет 70% grey.

После этого, дублируем (Ctrl+D) наш овал, заливаем черным цветом и уменьшаем клавишей (<).

Ну вот, один глаз звездочки готов, и осталось только перенести его на рисунок. Для этого нужно его сгруппировать. Выделяем оба овала и группируем – меню «Объект — Сгруппировать» или сочетанием клавиш (Ctrl+G). Теперь можно легко перенести глаз на рисунок, но перед этим немного уменьшить и повернуть.

Второй глаз мы получим, просто продублировав уже готовый.

Итак, у нас уже готова звездочка с глазами и для завершения рисунка рисуем пошагово улыбку. Для этого кривыми Безье рисуем треугольник, такой примерно формы как на рисунке.

Из созданного треугольника, при помощи узлов, делаем форму улыбки и заливаем черным цветом. Остается только перенести улыбку на рисунок, повернув и уменьшив ее «под рисунок звездочки».
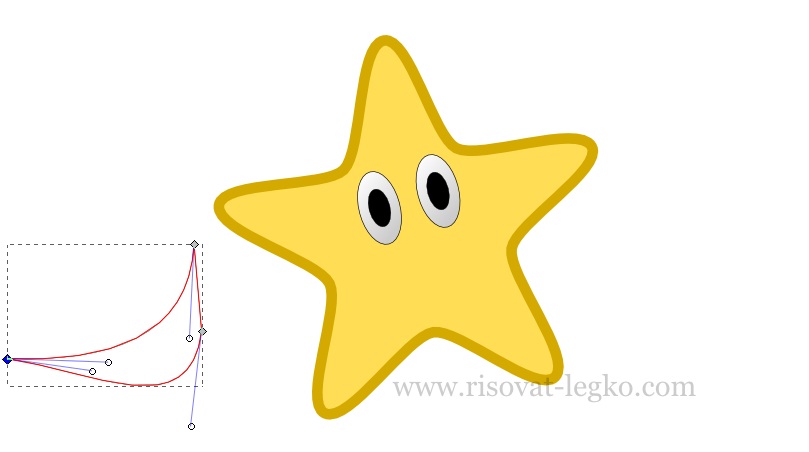
С остальными двумя фигурами — уголками рта звездочки, я предлагаю вам справиться самостоятельно. Они рисуются точно также как и улыбка, только немножко другой формы – треугольник кривыми Безье, а затем, при помощи узлов, делаете нужную вам форму.
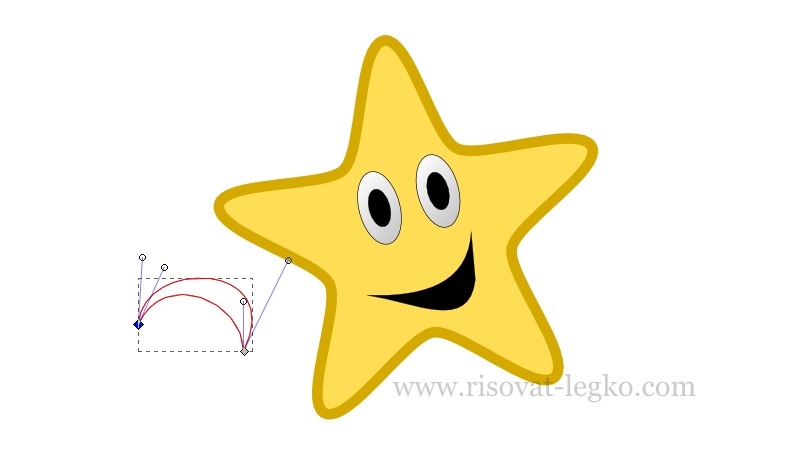
Уверен, что вы легко справились с уроком — рисуем пошагово звездочку потому, что в нем нет абсолютно ничего сложного.
Как рисовать облака и солнце поэтапно в Inkscape
Как рисовать облака

Итак, конечно же начинаем с облака, которое рисуется очень просто. Для его создания нам нужно много овалов. Выделяем нарисованные овалы и при помощи операции «Сумма» (Ctrl++) образуется облако. На рисунке снизу я отобразил описание — как рисовать облака.

Далее добавляем обводку, ширину которой вы можете подобрать по своему вкусу.
Теперь раскрашиваем наше готовое облако и его обводку при помощи линейного градиента. У обводки, так же как и у заливки, есть градиенты.
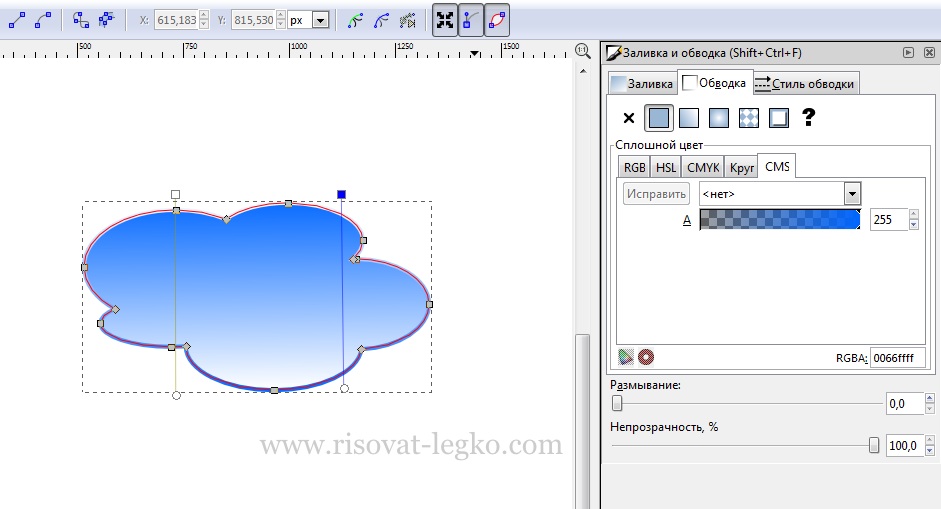
Сначала заливаем облако – вертикально ставим линейный градиент и придаем верхней точке синий цвет, нижней точке белый цвет.
Если присмотреться к рисунку ниже, то можно увидеть, что градиент обводки другого цвета – это позволяет не перепутать их. Также вертикально ставим градиент обводки и придаем цвета как у облака, но в точности наоборот – верхней точке белый цвет, нижней точке синий.
Рисуем солнце
Вы уже узнали, как рисовать облака, и далее рисуем солнце. Облако опустите вниз – оно пока нам не пригодится. Выбрав инструмент «Рисовать звезды и многоугольники» нужно немного втянуть звезду, потянув за внутренний узел.
В окошке «Углы» меняем количество углов на пятьдесят. Можете больше или меньше, но обязательно, углов должно быть четное количество.

Далее нам нужно оконтурить объект – меню «Контур – Оконтурить объект» или клавишами (Shift+Ctrl+С)
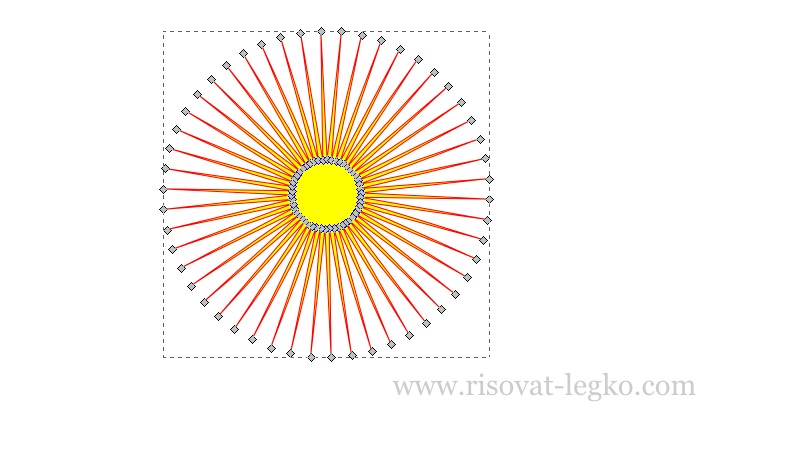
Увеличиваем масштаб, чтобы были хорошо видны узлы и удаляем каждый второй внутренний узел. Если все получилось, то должна быть вот такая картина как на рисунке.
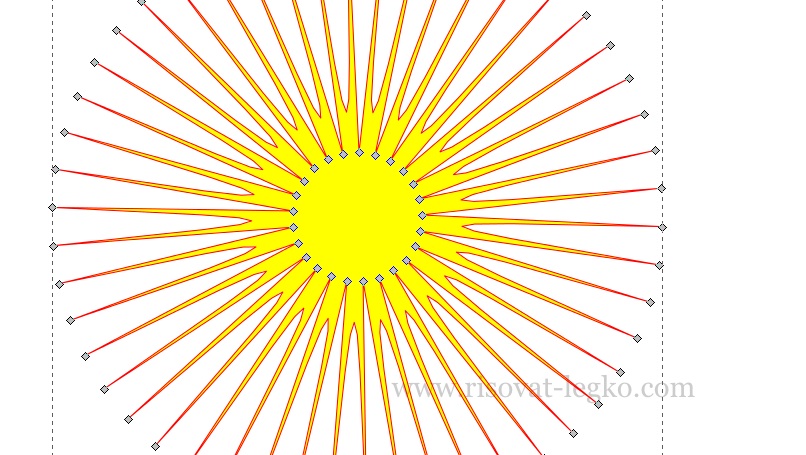
Поднимаем рычаги верхних узлов, как показано на рисунке.
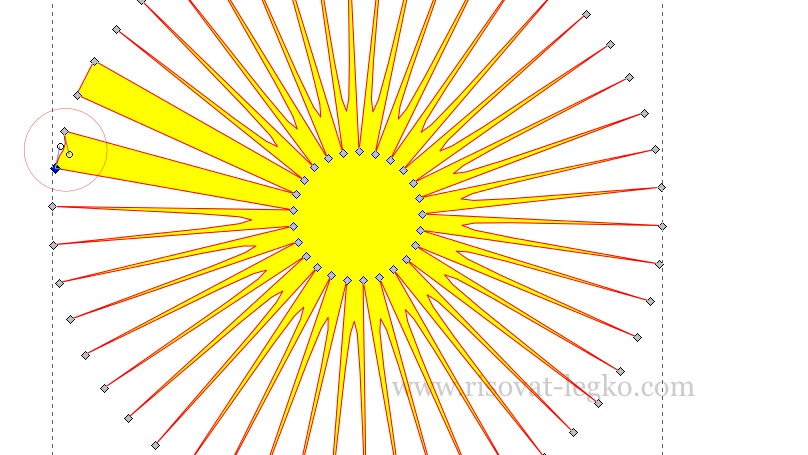
Нужно поднять все рычаги верхних узлов поочередно. Как вы, наверное, уже заметили, на рисунке рычаги подняты не ровно – делать их ровными необязательно и далее вы поймете почему.
.jpg)
Выбираем радиальный градиент и боковым точкам придаем значение прозрачности 100%. Центральная же точка остается непрозрачной.
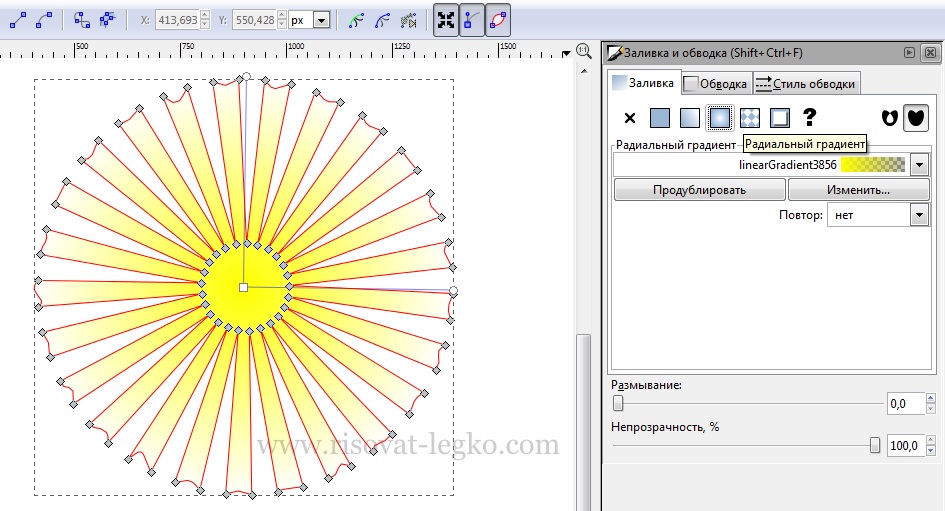
Убираем градиент – солнце готово!
Переместить солнце к облаку, я думаю, не составит труда. У меня на конечном рисунке присутствует фон, и если вы тоже хотите его создать, то нарисуйте прямоугольник и залейте линейным градиентом от белого, до светло-синего цвета. Клавишей (End) опустите на задний план. Поэкспериментируйте с цветом фона – это интересно.
Операции div, mod
Составить программу, которая вычисляет сумму трёх целых чисел
Запишите результат, выполнив фрагмент программы
Составить программу, которая вычисляет сумму цифр данного трёхзначного числа
Команды ввода и вывода. Команда присваивания
Составить программу, вычисляющую периметр прямоугольника
Советы по рисованию фигур в Inkscape
Как создать новый документ в Inkscape
Советы по рисованию фигур в Inkscape
Как рисовать прямоугольники и квадраты в Inkscape
Как рисовать круги, эллипсы и дуги в Inkscape
Как рисовать спирали в Inkscape
Как рисовать звезды и многоугольники в Inkscape
Создание и редактирование фигур
Создание и редактирование векторного изображения
- удалять клавишей Delete
- наклонять
- поворачивать
- отражать горизонтально( клавиша H) и вертикально (клавиша V)
- масштабировать
- перемещать в рабочей области
Создание и редактирование векторного изображения
- Выберите команду Файл - Открыть (или Ctrl + O)
- Выберите папку, содержащую нужный файл.
- Выделите файл и нажмите кнопку Открыть
- Выберите команду Файл - Сохранить как... ( или Ctrl +S).
- Выберите папку, в которую должен быть сохранён файл
- В поле Имя файла введите имя укажите имя файла и нажмите кнопку Сохранить
- Портрет
- Альбом
Понятие векторной графики
В зависимости от способа представления в памяти компьютерную графику можно разделить на два вида: растровую и векторную.
Векторное изображение — совокупность геометрических объектов (круги, эллипсы, отрезки и т.д.) и описаний параметров объектов, определяющих их внешний вид и взаимное расположение.
Основные цвета разбиваются на оттенки по яркости — от темного к светлому. Каждому оттенку присваивается числовое значение (например, самому темному — 0, самому светлому — 255).
- создание изображения;
- редактирование изображения;
- сохранения изображения в виде файла;
- загрузка изображения из файла в оперативную память;
- печать изображения
.svg — формат, который использует редактор Inkscape;
.eps — формат, обеспечивающий высокое качество рисунка;
.png — растровый формат изображений, поддерживающий прозрачность фона;
.bmp — несжатый растровый формат изображений;
.pdf — формат обмена документов от Adobe, который может содержать любые сочетания: текст, шрифты, растровую и векторную графику.
Операционная система
- запуск и выполнение всех процессов и программ;
- управление хранением информации;
- управление работой всех устройств компьютера;
- взаимодействие пользователя с компьютером.
- MS DOS;
- MS WINDOWS(XP,7,8,10);
- Unix;
- Linux;
- Apple Mac Os
- Рабочий стол;
- Панель задач;
- меню кнопки Пуск;
- окна;
- значки;
- ярлыки.
- компьютер;
- корзина;
- сетевое окружение;
- мои документы;
- проводник.
Окно программы появляется после запуска программы.
- Диалоговые окна предназначены для организации диалога пользователя с компьютером
- В окне справочной системы можно получить справку о работе программы
- Кнопка Пуск
- Значки загруженных программ и открытых папок
- Индикатор даты и времени
- Индикатор языка
- Индикатор сетевых подключений
- Регулятор громкости звука.
Путь начинается с корневой папки (имени диска) и содержит последовательность имен папок, в которые вложен файл. Диски именуются большими буквами английского алфавита с двоеточием после буквы. Имена дисков начинаются с C:. После имени каждой папки ставится обратный слэш.
- Поиск
- Копировать
- Переместить
- Вставить
- Удалить
- Переименовать
- Создать новую папку
- Создайте рисунок в графическом редакторе Paint с эмблемой класса. Сохраните файл в папке Рисунки с именем Эмблема.
- Создайте текстовый документ Расписание уроков. Сохраните файл с именем Расписание уроков в папке Тексты
- Создайте пейзаж в графическом редакторе Paint. Сохраните файл в папке Рисунки с именем Пейзаж.
- Создайте текстовый документ со списком учителей работающих в вашем классе. Сохраните файл с именем Список учителей в папке Тексты
Современные компьютерные устройства
Мейнфреймы - большой универсальный высокопроизводительный отказоустойчивый сервер со значительными ресурсами ввода-вывода, большим объёмом оперативной и внешней памяти, предназначенный для использования в критически важных системах (англ. mission-critical) с интенсивной пакетной и оперативной транзакционной обработкой.
Карманные компьютеры - портативное вычислительное устройство, обладающее широкими функциональными возможностями. КК часто называют наладонником (англ. palmtop) из-за небольших размеров.
Системный блок (англ. computer case, сленг. системник) — физически представляет собой шасси, которое наполнено аппаратным обеспечением для создания компьютера.
- Системная плата: (процессор, ОЗУ,ПЗУ, видеокарта, звуковая карта, сетевая карта
- Винчестер
- Блок питания
- Дисководы
- Модем
Операции над множествами
Два множества А и В равны (А=В), если они состоят из одних и тех же элементов.
Например, если А={1,2,3,4}, B={3,1,4,2} то А=В.
Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В.
Например, если А={1,2,4}, B={3,4,5,2}, то А ∩ В = {2,4}
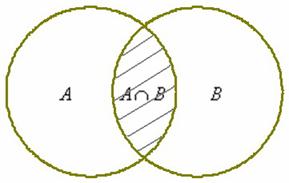
Объединение множеств характеризуется логической связкой ИЛИ и обозначается значком ∪
Например, если А={1,2,4}, B={3,4,5,6}, то А ∪ B = {1,2,3,4,5,6}
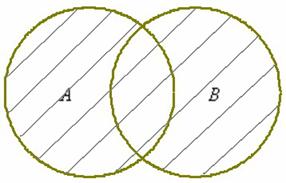
Разностью множеств А и В называют множество А\В, каждый элемент которого принадлежит множеству А и не принадлежит множеству В.
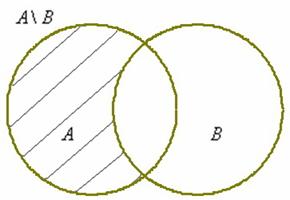
- А ∪ В
- А ∩ В
- C ∩ B
- A ∪ D
- (A ∩ C) ∪ (B ∩ C)
- А ∪ В
- А ∩ В
Множества
Множество – это совокупность объектов (элементов), которые понимаются как единое целое. Объекты, составляющие множества, называются элементами множества.
Множества обозначаются прописными буквами латинского алфавита: A, B, X, Y, A1, A2, …, элементы множеств – строчными буквами: a, b,x, y, a1, a2, … .
Множества бывают:
- конечные; частный случай – единичное (одно элементное) множество, например, множество преподавателей в этой аудитории, или множество десятичных цифр;
- бесконечные; пример – множество натуральных чисел;
- пустое {Ø}. Пустым множеством называют множество, не содержащее ни одного элемента.
а ∈ М (элемент а принадлежит множеству М), а ∉ М(элемент а не принадлежит множеству М). Если множество M состоит из элементов a, b, c, то это записывают так: M = {a, b, c}.
Множество В является подмножеством множества А, если каждый элемент множества В принадлежит множеству А. Иными словами, множество В содержится во множестве А, Обозначается: В ⊂ А. Значок ⊂ называют значком включения. Пример: {1,2,3}⊂ {1,2,3,4,5,6}/Запись А ⊄ М обозначает, что множество А не является подмножеством множества М.
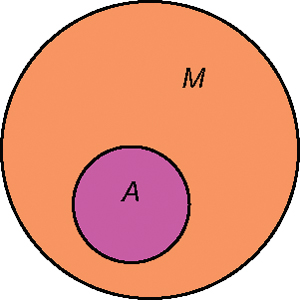
- В = {клавиатура, сканер, web-камера};
- С = {монитор, принтер, наушники};
- D = {дискета, CD-RW, DVD-RW }.
Задание 2. Удалите лишний элемент в каждом множестве
- В = {процессор, винчестер, оперативная память, дискета)};
- С = {монитор, принтер, системный блок, клавиатура};
- D = {принтер, клавиатура, сканер, web-камера}.
- Множество натуральных чисел.
- Множество акул в реке Днепр.
- Множество людей на Солнце.
- Множество натуральных чисел.
- Множество двухзначных чисел, меньших 9.
- Множество чисел (А) и множество натуральных чисел (В).
- Множество стран мира (М) и множество стран Европы (Е).
- Множество лиственных деревьев (С) и множество деревьев (Р).
- Множество квадратов (К) и множество прямоугольников (П).
- Множество носителей информации.
- Множество четных чисел.
- Множество обитателей рек.
- Множество молочных продуктов.
Логические операции И, ИЛИ
Составное высказывание А И В, образованное в результате объединения двух простых высказываний А и B логической операцией И, истинно тогда и только тогда, когда А и В одновременно истинны. Если хотя бы одно из простых высказываний, связанных операцией И, будет ложным, то и составное высказывание будет ложным. Для записи логической операции И используют следующие обозначения: A И B, A AND B, A · B, A * B, A∧ B, A & B.
| А | В | А и В |
| И | И | И |
| И | Л | Л |
| Л | И | Л |
| Л | Л | Л |
Составное высказывание А ИЛИ В, образованное в результате объединения двух простых высказываний А и B логической операцией ИЛИ, ложно тогда и только тогда, когда А и В одновременно ложны. Составное высказывание А ИЛИ В будет истинным, если истинно хотя бы одно из двух составляющих его простых высказываний. Для записи логической операции ИЛИ можно использовать следующие выражения: A ИЛИ B, A OR B, A + B, A∨ B, A | B.
| А | В | А или В |
| И | И | И |
| И | Л | И |
| Л | И | И |
| Л | Л | Л |
- Сосна - хвойное дерево, И кедр - не хвойное дерево.
- Принтер - устройство вывода информации ИЛИ клавиатура - устройство ввода информации.
- Мяч - круглый И Карась - рыба.
- Соловей - перелётная птица ИЛИ щука - морская рыба.
- 45 - четное число
- 20 > 7 ИЛИ 8<20
- Иногда во время дождя бывает радуга
- Акула - хищная рыба И зимой - холодно.
Логика высказываний
|
Логика высказываний
Теоретический материал
Высказывание — повествовательное предложение (утверждение), о котором в настоящее время можно сказать, истинно оно или ложно.
Истинное высказывание - высказывание, в котором заключена правдивая информация.
Ложное высказывание - высказывание, в котором заключена неверная информация.
Составные высказывания - высказывания, которые состоят из простых высказываний, соединенных друг с другом логическими операциями И, ИЛИ, НЕ.
Все дети - ученики (ложно)
Логическая операция НЕ (отрицание или инверсия) меняет значение высказывания на противоположное: истинно на ложно, а ложно на истинно. Логическое отрицание получается из высказывания путем добавления частицы «не» к сказуемому или с использованием оборота «неверно, что…» Если высказывание содержит слова «все», «всякий», «любой», то отрицание такого высказывания строится с использованием слов «некоторые», «хотя бы один». И наоборот, для высказываний со словами «некоторые», «хотя бы один» отрицание будет содержать слова «все», «всякий», «любой». Для записи логической операции НЕ можно использовать следующие выражения: НЕ А, Not A, ¬A, ~A. Высказывание и его отрицание никогда не могут быть истинными или ложными одновременно. Таблица истинности:
Видео Логика высказываний
Практическая часть
Задание 1. Выберите предложения, которые являются высказываниями:
Задание 2. Определите, истинными (И) или ложными (Л) являются высказывания с логической операцией НЕ.
Задание 3. Вставьте слова "все", "не все" так, чтобы высказывания стали истинными.
Электронная рабочая тетрадь
Проверка знаний
|
Информация и её свойства. Представление информации в компьютере
Код - совокупность условных знаков, каждому из которых присваивается определенное значение
Байт - единица измерения количества информации, состоящая из восьми последовательных и взаимосвязанных битов.
Для обозначения большего объема информации используются другие единицы измерения:
1 Кбайт (килобайт) = 1 024 байт;
1 Мбайт (мегабайт) = 1 024 Кбайт = 1 048 576 байт;
1 Гбайт (гигабайт) = 1 024 Мбайт = 1 048 576 Кбайт = 1 073 741 824 байт;
1 Тбайт (терабайт) = 1 024 Гбайт = 1 048 576 Мбайт = 1 073 741 824 Кбайт = 1 099 511 627 776 байт.
- 34 байта в биты;
- 128 Кбайт в байты;
- 4685638 Мбайт в Гбайт.
- 10 032 бит в байты